Whirlpool Dynamics: The physics of trub removal
Whirlpooling is a method for separating trub from wort that is widely used by homebrewers and commercial brewers. In commercial breweries, trub-containing wort is pumped tangentially into a tank with a flow rate that is sufficient to initially induce a spinning, circular flow pattern. As wort is pumped into the tank, the suspended trub moves along with the liquid, but when the pumping is stopped, the trub collects into a cone-shaped pile in the middle of the vessel. Homebrewers achieve this same whirlpool effect by rapidly stirring their wort in a circular motion and then stopping.
But why does the trub collect in the middle of the vessel? Why doesn’t it move outward and collect against the wall of the vessel? In order to explain why trub moves to the center of the tank instead of to the edges, we must first understand the details of the fluid dynamics that are at work within the system.
To explain how this phenomena works I will use the representative physical system of loose leaves being stirred in a teacup and discuss the physical forces at work within it. When the tea is stirred, the leaves are rotating around the bottom of a cup, following the motion of the water that is caused by stirring. When the stirring is stopped and the spoon is removed, the leaves begin to move towards the center of the cup and collect on the bottom, exactly like a brewer’s trub collects in the center of the whirlpool. When the tea is being stirred, the liquid level (and pressure) near the side walls of the cup or brewing vessel is higher than the liquid level in the center when the tea is rotating. The concave surface of the tea is evidence of this. This level and pressure variation is the result of the centripetal acceleration that balances the centrifugal acceleration of the rotating liquid. It is this pressure gradient that induces a vortex effect within the system, and this vortex causes the solids to move to the center of the rotating liquid.
The pressure gradient within the liquid exists because liquid near the bottom and sides of the cup cannot move as freely as the rest of the liquid within the cup. The liquid moves much more slowly near the bottom and sides of the cup because of frictional resistance. The net result of this fluid friction is that the angular momentum of the liquid near the bottom is not enough to oppose the effect of the radial pressure field created by the rotating liquid away from the bottom boundary layer. The pressure variation is such that it pushes the liquid (and any entrained solids) near the bottom of the cup towards the center. Because mass flow is conserved, the liquid moving towards the center of the cup then collides with liquid from the opposite side of the cup and turns upward towards the surface. When the liquid is near the surface, it then turns towards the side wall and finally moves down towards the bottom, replenishing the liquid that was originally there. The tea leaves recirculate with the water and eventually become entangled with one another near the bottom-center of the cup.
Eventually the solids clump together enough so that the upward movement of the liquid near the center is no longer sufficient to create a buoyant force that can overcome the force of gravity acting upon the solids. When this happens, the solids remain on the bottom and at the center of the cup.
The Tempest in the Teacup
A vortex is induced because liquid near the top of the vessel is pushed out “harder” because there is less fluid friction at the top of the liquid. The liquid near the bottom of the vessel is pushed out less because there is more friction and less force near the bottom to push it out. The weaker force at the bottom of the vessel induces a pressure gradient that creates an inward, recirculating flow. This inward recirculation is usually called the Bödewadt layer, after the German scientist who described the motion of a rotating fluid over an infinite wall at rest. Albert Einstein, however, was the first to give an explanation of this phenomenon in 1926 in the case of the teacup and his explanation is also correct for trub in a whirlpool.
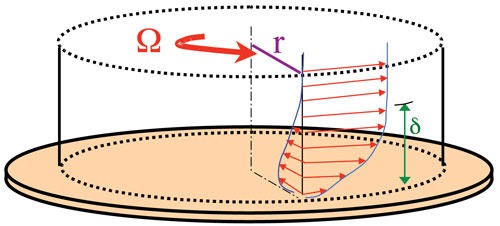
An illustration of the fluid flow situation within a system in which the fluid has been set into circular motion and then allowed to experience these frictional effects is shown in Figures 1a and 1b. The fluid slowed by wall friction is called a boundary layer, and this boundary layer plays a key role in the fluid mechanics of this system. The boundary layer thickness, δ, is given by the lengthscale where the imposed rotation Ω is diffused by viscosity in the intermediate fluid layers. In the ideal case of a fluid rotating over an infinite wall, the balance between centrifugal and viscous forces yields δ ~ (ν/Ω)1/2 (where ν is the kinematic viscosity of the fluid), which is a constant, independent of the radius r.

The mathematics describing this system are complex and involve solving numerous, simultaneous-differential equations. Thankfully, the power of modern computers coupled with commercially available computational fluid dynamics software is able to provide us with a good picture of the velocity profiles within our stirred teacup example. The velocity profiles for the stirred cup — seen in Figures 2 and 3 — are good analogues for what we could expect for velocity profiles within our trub-removing whirlpools.
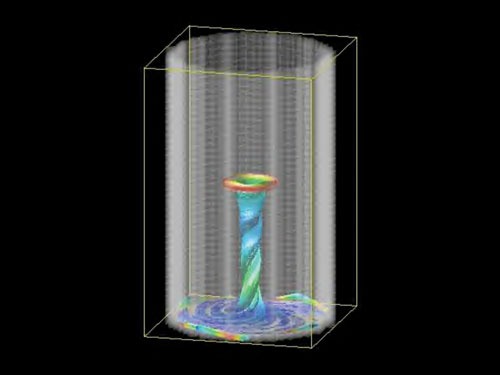
Figure 2 shows the velocity profiles for fluid flow near the bottom of the cup. Figure 3 shows velocity profiles across a cross-section of the cylindrical cup. In these figures, red represents relatively fast-moving fluid elements, and blue represents slower moving fluid elements. There are several factors that are important to consider when operating a whirlpool vessel: geometry, feed velocity and rotation time. Vessel geometry is an important consideration for a whirlpool vessel because it directly impacts the fluid dynamics within the system.

Commercial breweries usually use cylindrical or slightly cone-bottomed vessels with a depth:diameter ratio of between 1:1 to 1:5. Feed velocity and rotation time also affect the final results of the whirlpool. If the initial rotational velocity is too low, a poorly-compacted trub cone will be formed. If the initial rotational velocity is too high, the inertial forces caused by the fast-moving liquid may cause the trub cone to not hold together. Initial rotational velocities generally are determined by trial and error. Rotation time is important because all of the fluid-dynamic-induced forces must have time to work. Generally, commercial breweries allow a rotation time of between 10 and 40 minutes. Smaller tanks generally require less rotation time.
The optimum rotational velocity and rotation time for a homemade whirlpool system in your home brewery depends upon the geometry of your vessel, the amount of friction between the wort and your vessel and the clumping properties of the trub. It also depends slightly on the OG of your wort; whirlpool effectiveness decreases as the OG increases because the relative density differential between the wort and the trub decreases with increasing wort density. To ensure good cone formation within your whirlpool, add Irish moss or other flocculation aids and leave the vessel alone for at least 10 minutes.
Although it seems like a simple thing, a whirlpool is actually a very complex and dynamic system with multiple inertial, gravitational, viscous and friction forces all acting interdependently on the fluid elements within the wort. Optimization of this highly complex and dynamic system of forces within your own homebrewery will certainly require some experimentation. We are all fortunate in that the ability, freedom and desire to experiment is all part of what makes our homebrewing hobby great!


