Hot-Side Math: Geeking out on brewhouse efficiency

Understanding and measuring brewhouse efficiency is a very important skill to brewers. It is the beginning of understanding consistency. If you can’t brew with a consistent process you cannot properly evaluate your recipe changes. Brewhouse efficiency, as we are going to examine it, is the measure of how much of the potential sugars you extract from the malt measured once the boil kettle is full. An important goal is to be able to consistently hit the same efficiency with your brewhouse.
Calculating brewhouse efficiency is relatively simple but there are some inaccuracies that have to be considered if we are going to get a precise number. The numbers we must carefully measure are the weight of all of the grains and adjuncts used, the final volume of the wort collected, and the gravity of the wort collected. Often I see brewers trying to hit a target gravity with little concern to the final volume.
First we need to calculate the potential sugars available in the malts. Many brewers use recipe calculators to perform this task but there is something to be learned by doing this at least once by hand. The ideal specification to have is the coarse grind “as is” extract percentage from the maltster.
Let’s take a look at this malt spec and see what it means. Coarse grind is the closest mill setting to a brewer’s mill (often 0.7 mm on a slotted roller). The other spec would be fine grind (often 0.2 mm on a slotted roller) and it will always be higher than the coarse grind specification.
It is also important to understand the “as is” vs “dry basis” part of the spec. “As is” includes the moisture in the malt and the “dry basis” assumes all the water is removed. Since malt is usually about 5% moisture there is a difference in these numbers. Since we are going to weigh our malt without further drying it we prefer the “as is” specification. The other number we might find is the Fine to Coarse (F/C) ratio, an index of malt modification. It allows us to convert the fine extract to the coarse extract.
Calculating brewhouse efficiency is relatively simple but there are some inaccuracies that have to be considered if we are going to get a precise number.
If we have the “coarse grind as is” extract we will use it without adjustment. If we don’t, we can do some conversions to get a more realistic expectation of the extractable sugars:
Coarse Grind (dry) Extract x (1 – Moisture) = Coarse Grind (as is) Extract.
The worst case would be if we only have a fine grind dry and moisture content %. Because the F/C ratio is a variable, we don’t have enough information and we have to do a little guessing. Looking up a random Pilsner malt online I found these specs as an example:
Moisture content = 4.3%.
Extract, fine (dry) = 83.5%.
First, using the equation above, I can convert the dry to “as is”:
0.835 x 0.957 = 78% Extract, fine (as is)
Highly modified malts have an F/C ratio of 0.5–1%. We will take the 1% value if it is not on our spec sheet:
0.78 x 0.99 = 77%.
Now that we know the extract available we can get a more commonly used homebrewing number, extract potential, measured in points per gallon, or ppg. Extract potential is what we expect if we have 100% efficiency and extract all the sugars from 1 lb. (0.45 kg) of malt in 1 gallon (3.8 L) of water:
ppg = (Coarse Grind (as is) / 100) x 0.04621 + 1.
So, in our example:
ppg = (77%/100) x 0.0462 + 1 = 1.0356.
It is good for us to uncover where the constant 0.0462 found in this equation comes from. That is derived when one pound (0.45 kg) of sucrose is dissolved in one gallon (3.8 L) of water; the yielding solution will measure 1.046 SG. We can get this number alternatively from the density of sucrose (1.58 g/cm3, which I’ll leave it for the very advanced brewer) or we can measure it directly with a hydrometer.
Now we can start to see what our main extract is going to look like. If we can get 1.0356 in a perfect world and, for example, we only get 1.0285 we clearly lost some gravity points due to some form of an inefficiency. This equation is:
(Measured Gravity – 1)/(ppg – 1)
So for our case, we have: 0.0258 / 0.0356 = 72.5%.
This is a low, but an often-seen, efficiency range among all-grain homebrewers.
In an actual recipe we have different grains found at varying ratios, but the theory is the same as the example above. Let’s try one:
13 lbs. (5.9 kg) base malt at 1.036 ppg
1 lb. (0.45 kg) Carapils® at 1.026 ppg
1 lb. (0.45 kg) dextrose sugar at 1.046 ppg
in 5 gallons (19 L) of water
The one found in the 1.XXX of standard gravity measurements is always a problem with these calculations so we will remove it from our equation in the beginning and add it back at the end giving us:
(13 x 0.036) + (1 x 0.026) + (1 x 0.046) = 0.549
Next we divide by our volume: 0.549 / 5 gallons = 0.098 and add back the 1 to make specific gravity happy and we get a theoretical value of 1.098 for our recipe. Now once we mash and measure 1.082 and collect 4.75 gallons (18 L), what was our efficiency? Let’s figure that out:
Efficiency = [(OG – 1) / (predicted gravity – 1)] * (actual volume / desired volume)
Efficiency = (0.082 / 0.098) x (4.75 / 5) = 78% efficiency
It is the last correction that is often missed or incorrect in homebrewing. The actual volume measured is very important.
I use a stainless ruler to measure my volume. Simply add 5 gallons (19 L) (measured as carefully as you can) to your kettle and measure the height from the bottom to the top of the liquid. Then add 1 more gallon (4 L) and measure again (assuming you have straight walls.)
If you want to be very pedantic about this you can heat the water to your measuring temperature and then cool it to your serving temperature and calculate the apparent expansion of water in your kettle. In small batches the actual kettle’s expansion can be ignored. The change likely exceeds the measurement error from the yardstick.
Water has a non-linear expansion rate that strongly affects measuring temperature on the hot side.
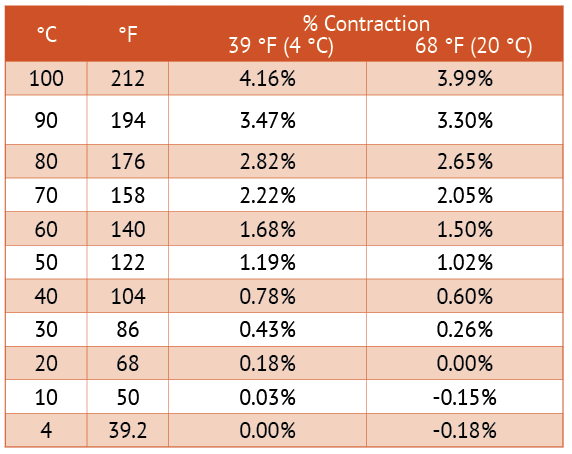
So our actual volume is: Actual Volume = Measured Volume x (1 – Percent Contraction)
Updating our equation: Efficiency = [(OG – 1) / (predicted gravity – 1)] x [(actual volume x (1-volume change)] / desired volume)
This lowers our efficiency to 77%.
Making A Difference
How can we affect this efficiency in our system? The most important parameter to get a hold of is mill gap. Different malts will need slightly different settings in order to get the best efficiency without sticking the mash. Mash screen design effects this parameter and this setting needs to be sorted out by trial and error for each mash tun design.
We also can control our mash pH, however I recommend the homebrewer sets this to 5.2–5.4 instead of the more efficient 5.8 because of flavor reasons. Grist-to-water ratio will change mash pH and also affect efficiency. Also, increasing sparge temperature will extract more sugars while sparge duration can also strongly affect efficiency. To put these in order of most important to least important, in my mind, for single infusion mashes with highly modified malts: Mill gap spacing, sparge duration, sparge temperature, grist/water ratio, mash pH, and finally mash screen design.
I include mash screen design last because once set it does not change. Keeping the other parameters constant will allow you to have consistent efficiencies in the mash and a more consistent brewhouse to experiment with recipe changes.
I strive to maintain about 80% efficiency in my system as I find that is a good balance between my time, an efficient use of raw materials, and flavor. In order to achieve that high of an efficiency I have to sparge more slowly for high-gravity beers. An important parameter here is grain bed depth. A deeper grain bed requires more time to sparge efficiently.
In a more advanced system with rakes and the ability to step mash we can gain further efficiency by controlling the additional parameters.
Boil Math
The next place we need to take control of is our boil. We know how much wort we collected and now we are going to boil it. If we are going to have a consistent product we need to control the evaporation rate. We can’t control what we can’t measure, so after the boil is finished we use our ruler and measure the final volume.
Holding the evaporation rate constant is very important because it changes the flavors of the malt as well as the gravity readings. For small changes you can make a consistent product by boiling a little more and watering back to the desired volume or the desired gravity. However, this only works for small corrections. An experienced taster should be able to taste a 2% change in evaporation rate between batches of the same recipe.
There are some numbers I like to keep in mind. Going below 9% evaporation rate should only be done with careful consideration of dimethyl sulfide. I have seen commercial processes with evaporation rates below 6% but only with extreme changes to a traditional brewhouse. Also, over 16% creates flavors from melanoidin production that are undesirable in many styles (although highly desired in others.) I have formulated all of my recipes around a 10% evaporation rate.
This leaves to the last a final bit of hot-side math. How do we calculate how to fix our missed gravity? If our gravity lands too high, we will use water to dilute the sugar levels back to the desired gravity:
Water Needed = [(Actual Volume x (Measured Gravity – Target Gravity)] / (Target Gravity – 1)
If our gravity lands too low, we will use light dried malt extract (DME) as it will change the flavors the least:
DME Needed (lbs.) = [Actual Volume x (Target Gravity – Actual Gravity)] / 0.045
The constant 0.045 is from the ppg of DME of 1 lb. (0.45 kg) of DME in 1 gallon (3.8 L) of water = 1.045 SG.
Whew, if you stuck in this far you have learned how your recipe calculator works, at least the gravity-side of the calculator. You can now calculate your efficiency and correct back to your recipe after boil. This is the beginning of creating a consistent brewing process and will allow you to learn how recipe changes affect the flavors of you beers without brewhouse parameters muddying up the waters.



